4. 集合和函数

集合、关系和函数的词汇为所有数学分支的构造提供了统一的语言。 由于函数和关系可以用集合来定义，因此公理集合论可以作为数学的基础。

作为 Lean 基础的原始概念则是 类型，它包括在类型间定义函数的方法。 Lean 中的每个表达式都有一个类型：自然数、实数、从实数到实数的函数、群、向量空间等等。 有的表达式 是 类型，也就是说，它们的类型是 Type. Lean 和 Mathlib 提供定义新类型的方式，以及定义这些类型的对象的方式。

从概念上讲，你可以把类型看作是一组对象的集合。 要求每个对象都有一个类型有一些好处。 例如，它使得重载像 + 这样的符号成为可能， 有时它还能缩减冗长的输入，因为 Lean 可以从对象的类型中推断出大量信息。 当你将函数应用于错误的参数个数， 或将函数应用于错误类型的参数时， 类型系统还让 Lean 可以标记错误。

Lean 的库确实定义了初等集合论概念。 与集合论不同的是，在 Lean 中，集合总是某种类型的对象和集合， 例如自然数集合或从实数到实数的函数的集合。 类型和集合之间的区别需要一些时间来适应，但本章将带你了解其中的要点。

4.1. 集合

若 α 是任意类型，则类型 Set α 由 α 中的元素组成的集合构成。 这一类型支持常规的集合论运算和关系。 例如， s ⊆ t 是说 s 是 t 的子集， s ∩ t 是指 s 和 t 的交集， 而 s ∪ t 是指它们的并集。 子集关系可以用 \ss 或 \sub 输入， 交集可以用 \i 或 \cap 输入， 并集可以用 \un 或 \cup 输入。 库中也定义了集合 univ, 它包含类型 α 的全部元素， 以及空集 ∅, 可以用 \empty 输入。 给定 x : α 和 s : Set α, 表达式 x ∈ s 是说 x 是 s 的一个成员。 提到集合成员关系的定理的名字经常含有 mem. 表达式 x ∉ s 是 ¬ x ∈ s 的缩写。 你可以用 \in 或 \mem 输入 ∈, 用 \notin 输入 ∉.

证明关于集合的事情的一种方法是使用 rw 或化简器来展开定义。 在下面的第二个例子中， 我们使用 simp only 告诉化简器只使用我们给它的列表中的等式， 而不是整个数据库中的等式。 不同于 rw, simp 可以在全称或存在量词内实施化简。 如果你逐步查看证明，你可以看到这些命令的效果。

variable {α : Type*}
variable (s t u : Set α)
open Set

example (h : s ⊆ t) : s ∩ u ⊆ t ∩ u := by
  rw [subset_def, inter_def, inter_def]
  rw [subset_def] at h
  simp only [mem_setOf]
  rintro x ⟨xs, xu⟩
  exact ⟨h _ xs, xu⟩

example (h : s ⊆ t) : s ∩ u ⊆ t ∩ u := by
  simp only [subset_def, mem_inter_iff] at *
  rintro x ⟨xs, xu⟩
  exact ⟨h _ xs, xu⟩

在这个例子中，我们开启了 Set 名字空间以用更短的定理名访问定理。 但事实上，我们可以完全删除 rw 和 simp 的调用：

example (h : s ⊆ t) : s ∩ u ⊆ t ∩ u := by
  intro x xsu
  exact ⟨h xsu.1, xsu.2⟩

这里发生的事情被称为 定义约化：为了理解 intro 命令和匿名构造函数， Lean 不得不展开定义。 下面的例子也说明了这一现象：

example (h : s ⊆ t) : s ∩ u ⊆ t ∩ u :=
  fun x ⟨xs, xu⟩ ↦ ⟨h xs, xu⟩

为了处理并集，我们可以使用 Set.union_def 和 Set.mem_union. 由于 x ∈ s ∪ t 展开为 x ∈ s ∨ x ∈ t, 我们也可以使用 cases 策略强制要求定义约化。

example : s ∩ (t ∪ u) ⊆ s ∩ t ∪ s ∩ u := by
  intro x hx
  have xs : x ∈ s := hx.1
  have xtu : x ∈ t ∪ u := hx.2
  rcases xtu with xt | xu
  · left
    show x ∈ s ∩ t
    exact ⟨xs, xt⟩
  · right
    show x ∈ s ∩ u
    exact ⟨xs, xu⟩

由于交集比联合更紧密， 表达式 (s ∩ t) ∪ (s ∩ u) 中使用括号是不必要的， 但它们使表达式的含义更清晰。 下面是对同一事实更简短的证明：

example : s ∩ (t ∪ u) ⊆ s ∩ t ∪ s ∩ u := by
  rintro x ⟨xs, xt | xu⟩
  · left; exact ⟨xs, xt⟩
  · right; exact ⟨xs, xu⟩

作为练习，试着证明另一方向的包含关系：

example : s ∩ t ∪ s ∩ u ⊆ s ∩ (t ∪ u) := by
  sorry

知道以下事实可能有帮助：当使用 rintro 时， 有时我们需要使用括号包围析取模式 h1 | h2 使得 Lean 能正确解析它。

库里也定义了集合的差， s \ t, 其中反斜线是以 \\ 输入的特殊unicode字符。 表达式 x ∈ s \ t 展开为 x ∈ s ∧ x ∉ t. （ ∉ 可以用 \notin 输入。） 可以使用 Set.diff_eq 和 dsimp 或 Set.mem_diff 手动重写它， 而下面对同一个包含关系的两个证明展示了如何避免使用它们。

example : (s \ t) \ u ⊆ s \ (t ∪ u) := by
  intro x xstu
  have xs : x ∈ s := xstu.1.1
  have xnt : x ∉ t := xstu.1.2
  have xnu : x ∉ u := xstu.2
  constructor
  · exact xs
  intro xtu
  -- x ∈ t ∨ x ∈ u
  rcases xtu with xt | xu
  · show False; exact xnt xt
  · show False; exact xnu xu

example : (s \ t) \ u ⊆ s \ (t ∪ u) := by
  rintro x ⟨⟨xs, xnt⟩, xnu⟩
  use xs
  rintro (xt | xu) <;> contradiction

作为练习，证明反向的包含关系：

example : s \ (t ∪ u) ⊆ (s \ t) \ u := by
  sorry

要证明两个集合相等， 只需证明任一集合中的每个元素都是另一个集合中的元素。 这个原理称为“外延性”，毫不意外的是， ext 策略可以用于处理它。

example : s ∩ t = t ∩ s := by
  ext x
  simp only [mem_inter_iff]
  constructor
  · rintro ⟨xs, xt⟩; exact ⟨xt, xs⟩
  · rintro ⟨xt, xs⟩; exact ⟨xs, xt⟩

再次重申，删除 simp only [mem_inter_iff] 一行并不会损害证明。 事实上，如果你喜欢高深莫测的证明项，下面的单行证明就是为你准备的：

example : s ∩ t = t ∩ s :=
  Set.ext fun x ↦ ⟨fun ⟨xs, xt⟩ ↦ ⟨xt, xs⟩, fun ⟨xt, xs⟩ ↦ ⟨xs, xt⟩⟩

这是一个更简短的证明，使用了化简器：

example : s ∩ t = t ∩ s := by ext x; simp [and_comm]

除了使用 ext 之外，我们还可以使用 Subset.antisymm 这个定理， 它可以通过证明 s ⊆ t 和 t ⊆ s 来证明集合间的等式 s = t.

example : s ∩ t = t ∩ s := by
  apply Subset.antisymm
  · rintro x ⟨xs, xt⟩; exact ⟨xt, xs⟩
  · rintro x ⟨xt, xs⟩; exact ⟨xs, xt⟩

尝试完成证明项：

example : s ∩ t = t ∩ s :=
    Subset.antisymm sorry sorry

请记住，您可以用下划线代替 sorry, 并将鼠标悬停在它上面, Lean 会向你显示它在这一位置的预期。

下面是一些你可能会喜欢证明的集合论性质：

example : s ∩ (s ∪ t) = s := by
  sorry

example : s ∪ s ∩ t = s := by
  sorry

example : s \ t ∪ t = s ∪ t := by
  sorry

example : s \ t ∪ t \ s = (s ∪ t) \ (s ∩ t) := by
  sorry

说到集合的表示，下面就为大家揭秘背后的机制。 在类型论中，类型 α 上的 性质 或 谓词 只是一个函数 P : α → Prop. 这是有意义的：给定 a : α, P a 就是 P 对 a 成立这一命题。 在库中， Set α 定义为 α → Prop 而 x ∈ s 定义为 s x. 换句话说，集合实际上就是性质，只是被当成对象。

库中也定义了集合构造器的符号。 表达式 { y | P y } 展开就是 (fun y ↦ P y), 因此 x ∈ { y | P y } 约化为 P x. 因此我们可以把偶数性质转化为偶数集合：

def evens : Set ℕ :=
  { n | Even n }

def odds : Set ℕ :=
  { n | ¬Even n }

example : evens ∪ odds = univ := by
  rw [evens, odds]
  ext n
  simp [-Nat.not_even_iff_odd]
  apply Classical.em

你应该逐步跟踪这个证明， 确定你明白发生了什么。 注意到我们告诉化简器 不要 使用引理 Nat.not_even_iff, 因为我们想要把 ¬ Even n 留在我们的目标中。 尝试删除 rw [evens, odds] 这一行， 确认证明仍然成立。

事实上，集合构造器符号定义

• s ∩ t 为 {x | x ∈ s ∧ x ∈ t},

• s ∪ t 为 {x | x ∈ s ∨ x ∈ t},

• ∅ 为 {x | False}, 以及

• univ 为 {x | True}.

我们经常需要精确指定 ∅ 和 univ 的类型， 因为 Lean 很难猜出我们指的是哪种类型。 下面的例子演示了当需要的时候 Lean 如何展开最后两个定义。 在第二个例子中， trivial 是 库中对 True 的标准证明。

example (x : ℕ) (h : x ∈ (∅ : Set ℕ)) : False :=
  h

example (x : ℕ) : x ∈ (univ : Set ℕ) :=
  trivial

作为练习，证明下列包含关系。 使用 intro n 以展开子集定义， 使用化简器把集合论构造约化为逻辑。 我们也推荐使用定理 Nat.Prime.eq_two_or_odd 和 Nat.odd_iff.

example : { n | Nat.Prime n } ∩ { n | n > 2 } ⊆ { n | ¬Even n } := by
  sorry

请注意：有点令人困惑的是，库中有多个版本的谓词 Prime. 最通用的谓词对任何有零元素的交换幺半群都有意义。 谓词 Nat.Prime 是针对自然数的。 幸运的是，有一个定理指出，在特定情况下， 这两个概念是一致的，所以你总是可以把一个谓词改写成另一个谓词。

#print Prime

#print Nat.Prime

example (n : ℕ) : Prime n ↔ Nat.Prime n :=
  Nat.prime_iff.symm

example (n : ℕ) (h : Prime n) : Nat.Prime n := by
  rw [Nat.prime_iff]
  exact h

rwa 策略是在重写后跟着一个假设策略。

example (n : ℕ) (h : Prime n) : Nat.Prime n := by
  rwa [Nat.prime_iff]

Lean 引入了记号 ∀ x ∈ s, ..., “对于任意 x 属于 s .,” 作为 ∀ x, x ∈ s → ... 的简化。 Lean 还引入了记号 ∃ x ∈ s, ..., “存在 x 属于 s 使得 ..” 有时它们被称为 有界量词, 因为这种构造将它们的意义限制在集合 s 内。 因此，库中使用这些量词的定理通常在名称中包含 ball 或 bex. 定理 bex_def 断言 ∃ x ∈ s, ... 等价于 ∃ x, x ∈ s ∧ ..., 但当它们和 rintro, use 以及匿名构造器一起使用时， 这两个表达式的行为大致相同。 因此，我们通常不需要使用 bex_def 来精确转换它们。 这是关于它们用法的一些例子：

variable (s t : Set ℕ)

example (h₀ : ∀ x ∈ s, ¬Even x) (h₁ : ∀ x ∈ s, Prime x) : ∀ x ∈ s, ¬Even x ∧ Prime x := by
  intro x xs
  constructor
  · apply h₀ x xs
  apply h₁ x xs

example (h : ∃ x ∈ s, ¬Even x ∧ Prime x) : ∃ x ∈ s, Prime x := by
  rcases h with ⟨x, xs, _, prime_x⟩
  use x, xs

看看你能否证明这些略有不同的版本：

section
variable (ssubt : s ⊆ t)

example (h₀ : ∀ x ∈ t, ¬Even x) (h₁ : ∀ x ∈ t, Prime x) : ∀ x ∈ s, ¬Even x ∧ Prime x := by
  sorry

example (h : ∃ x ∈ s, ¬Even x ∧ Prime x) : ∃ x ∈ t, Prime x := by
  sorry

end

带下标的并集和交集是另一种重要的集合论构造。 我们可以把 α 中的元素组成的集合的序列 \(A_0, A_1, A_2, \ldots\) 建模为函数 A : ℕ → Set α, 此时 ⋃ i, A i 表示它们的并集， 而 ⋂ i, A i 表示它们的交集。 这里自然数没有什么特别之处，因此 ℕ 可以替换为任意作为指标集的类型 I. 下面说明它们的用法。

variable {α I : Type*}
variable (A B : I → Set α)
variable (s : Set α)

open Set

example : (s ∩ ⋃ i, A i) = ⋃ i, A i ∩ s := by
  ext x
  simp only [mem_inter_iff, mem_iUnion]
  constructor
  · rintro ⟨xs, ⟨i, xAi⟩⟩
    exact ⟨i, xAi, xs⟩
  rintro ⟨i, xAi, xs⟩
  exact ⟨xs, ⟨i, xAi⟩⟩

example : (⋂ i, A i ∩ B i) = (⋂ i, A i) ∩ ⋂ i, B i := by
  ext x
  simp only [mem_inter_iff, mem_iInter]
  constructor
  · intro h
    constructor
    · intro i
      exact (h i).1
    intro i
    exact (h i).2
  rintro ⟨h1, h2⟩ i
  constructor
  · exact h1 i
  exact h2 i

带下标的并集或交集通常需要使用括号， 因为与量词一样，绑定变量的范围会尽可能地扩展。

尝试证明下列恒等式。 其中一个方向需要经典逻辑！ 我们建议在证明的适当位置使用 by_cases xs : x ∈ s.

example : (s ∪ ⋂ i, A i) = ⋂ i, A i ∪ s := by
  sorry

Mathlib 也有有界并集和有界交集，它们类似于有界量词。 您可以使用 mem_iUnion₂ 和 mem_iInter₂ 揭示它们的含义。 正如下面的示例所示，Lean 的化简器也可以执行这些替换。

def primes : Set ℕ :=
  { x | Nat.Prime x }

example : (⋃ p ∈ primes, { x | p ^ 2 ∣ x }) = { x | ∃ p ∈ primes, p ^ 2 ∣ x } :=by
  ext
  rw [mem_iUnion₂]
  simp

example : (⋃ p ∈ primes, { x | p ^ 2 ∣ x }) = { x | ∃ p ∈ primes, p ^ 2 ∣ x } := by
  ext
  simp

example : (⋂ p ∈ primes, { x | ¬p ∣ x }) ⊆ { x | x = 1 } := by
  intro x
  contrapose!
  simp
  apply Nat.exists_prime_and_dvd

试着解决下面这个类似的例子。 如果你开始输入 eq_univ, 标签补全器会告诉你 apply eq_univ_of_forall 是开始证明的好方法。 我们还推荐使用 Nat.exists_infinite_primes 定理。

example : (⋃ p ∈ primes, { x | x ≤ p }) = univ := by
  sorry

给定一组集合 s : Set (Set α), 它们的并集 ⋃₀ s 具有类型 Set α, 定义为 {x | ∃ t ∈ s, x ∈ t}. 类似地，它们的交集 ⋂₀ s 定义为 {x | ∀ t ∈ s, x ∈ t}. 这些运算分别称为 sUnion 和 sInter. 下面的例子展示了它们与有界并集和有界交集的关系。

variable {α : Type*} (s : Set (Set α))

example : ⋃₀ s = ⋃ t ∈ s, t := by
  ext x
  rw [mem_iUnion₂]
  simp

example : ⋂₀ s = ⋂ t ∈ s, t := by
  ext x
  rw [mem_iInter₂]
  rfl

在库中，这些恒等式称为 sUnion_eq_biUnion 和 sInter_eq_biInter.

4.2. 函数

若 f : α → β 是一个函数，而 p 是一个类型为 β 的元素的集合， 则 Mathlib 库把 preimage f p (记为 f ⁻¹' p ) 定义为 {x | f x ∈ p}. 表达式 x ∈ f ⁻¹' p 约化为 f x ∈ p. 这经常很方便，就像在下面例子中看到的这样：

variable {α β : Type*}
variable (f : α → β)
variable (s t : Set α)
variable (u v : Set β)

open Function
open Set

example : f ⁻¹' (u ∩ v) = f ⁻¹' u ∩ f ⁻¹' v := by
  ext
  rfl

若 s 是类型为 α 的元素的集合， 库也把 image f s (记为 f '' s ) 定义为 {y | ∃ x, x ∈ s ∧ f x = y}. 从而假设 y ∈ f '' s 分解为三元组 ⟨x, xs, xeq⟩, 其中 x : α 满足假设 xs : x ∈ s 和 xeq : f x = y. rintro 策略中的 rfl 标签 (见 Section 3.2) 在这类情况下被明确了。

example : f '' (s ∪ t) = f '' s ∪ f '' t := by
  ext y; constructor
  · rintro ⟨x, xs | xt, rfl⟩
    · left
      use x, xs
    right
    use x, xt
  rintro (⟨x, xs, rfl⟩ | ⟨x, xt, rfl⟩)
  · use x, Or.inl xs
  use x, Or.inr xt

也请你注意到， use 策略使用了 rfl 以在可以做到时关闭目标。

这是另一个例子：

example : s ⊆ f ⁻¹' (f '' s) := by
  intro x xs
  show f x ∈ f '' s
  use x, xs

如果我们想使用专门为这个目的设计的定理， 那么我们可以把 use x, xs 这一行换成 apply mem_image_of_mem f xs. 但知道像是用存在量词定义的往往会带来方便。

下列等价关系是一个好练习题：

example : f '' s ⊆ v ↔ s ⊆ f ⁻¹' v := by
  sorry

它表明 image f 和 preimage f 是 Set α 和 Set β 之间所谓 伽罗瓦连接(Galois connection) 的一个实例， 每个实例都由子集关系作为偏序。 在库中，这个等价关系被命名为 image_subset_iff. 在实践中，右手边通常是更有用的表达方式， 因为 y ∈ f ⁻¹' t 展开为 f y ∈ t, 而处理 x ∈ f '' s 则需要分解一个存在量词。

这里有一长串集合论定理供您消遣。 你不必一次全部做完，只需做其中几个， 其余的留待一个空闲的雨天再做。

example (h : Injective f) : f ⁻¹' (f '' s) ⊆ s := by
  sorry

example : f '' (f ⁻¹' u) ⊆ u := by
  sorry

example (h : Surjective f) : u ⊆ f '' (f ⁻¹' u) := by
  sorry

example (h : s ⊆ t) : f '' s ⊆ f '' t := by
  sorry

example (h : u ⊆ v) : f ⁻¹' u ⊆ f ⁻¹' v := by
  sorry

example : f ⁻¹' (u ∪ v) = f ⁻¹' u ∪ f ⁻¹' v := by
  sorry

example : f '' (s ∩ t) ⊆ f '' s ∩ f '' t := by
  sorry

example (h : Injective f) : f '' s ∩ f '' t ⊆ f '' (s ∩ t) := by
  sorry

example : f '' s \ f '' t ⊆ f '' (s \ t) := by
  sorry

example : f ⁻¹' u \ f ⁻¹' v ⊆ f ⁻¹' (u \ v) := by
  sorry

example : f '' s ∩ v = f '' (s ∩ f ⁻¹' v) := by
  sorry

example : f '' (s ∩ f ⁻¹' u) ⊆ f '' s ∩ u := by
  sorry

example : s ∩ f ⁻¹' u ⊆ f ⁻¹' (f '' s ∩ u) := by
  sorry

example : s ∪ f ⁻¹' u ⊆ f ⁻¹' (f '' s ∪ u) := by
  sorry

你还可以尝试下一组练习， 这些练习描述了像和原像在带下标的并集和交集中的性质。 在第三个练习中，参数 i : I 是必要的，因为要保证指标集非空。 要证明其中任何一个，我们推荐使用 ext 或 intro 展开等式或集合之间的包含关系的定义， 然后调用 simp 解包集合成员所需的条件。

variable {I : Type*} (A : I → Set α) (B : I → Set β)

example : (f '' ⋃ i, A i) = ⋃ i, f '' A i := by
  sorry

example : (f '' ⋂ i, A i) ⊆ ⋂ i, f '' A i := by
  sorry

example (i : I) (injf : Injective f) : (⋂ i, f '' A i) ⊆ f '' ⋂ i, A i := by
  sorry

example : (f ⁻¹' ⋃ i, B i) = ⋃ i, f ⁻¹' B i := by
  sorry

example : (f ⁻¹' ⋂ i, B i) = ⋂ i, f ⁻¹' B i := by
  sorry

Mathlib 库定义了谓词 InjOn f s, 表示 f 在 s 上是单射。 定义如下：

example : InjOn f s ↔ ∀ x₁ ∈ s, ∀ x₂ ∈ s, f x₁ = f x₂ → x₁ = x₂ :=
  Iff.refl _

可以证明语句 Injective f 等价于 InjOn f univ. 类似地， 库中将 range f 定义为 {x | ∃y, f y = x}, 因此可以证明 range f 等于 f '' univ. 这是 Mathlib 中的一个常见主题： 虽然函数的许多属性都是对于其完整域定义的， 但通常也有相对化版本，将语句限制为域类型的子集。

下面是一些使用 InjOn 和 range 的例子：

open Set Real

example : InjOn log { x | x > 0 } := by
  intro x xpos y ypos
  intro e
  -- log x = log y
  calc
    x = exp (log x) := by rw [exp_log xpos]
    _ = exp (log y) := by rw [e]
    _ = y := by rw [exp_log ypos]


example : range exp = { y | y > 0 } := by
  ext y; constructor
  · rintro ⟨x, rfl⟩
    apply exp_pos
  intro ypos
  use log y
  rw [exp_log ypos]

试证明：

example : InjOn sqrt { x | x ≥ 0 } := by
  sorry

example : InjOn (fun x ↦ x ^ 2) { x : ℝ | x ≥ 0 } := by
  sorry

example : sqrt '' { x | x ≥ 0 } = { y | y ≥ 0 } := by
  sorry

example : (range fun x ↦ x ^ 2) = { y : ℝ | y ≥ 0 } := by
  sorry

要定义函数 f : α → β 的反函数， 我们会式样两种新方法。 第一，我们需要处理 Lean 中任意类型可能为空这一事实。 为了在没有 x 满足 f x = y 时定义 f 的逆在 y 处的取值， 我们想要指定 α 中的缺省值。 将注释 [Inhabited α] 添加为变量等于假设 α 有一个默认元素， 即 default. 第二，当存在多于一个 x 满足 f x = y 时， 反函数需要 选择 其中一个。 这需要诉诸 选择公理。 Lean 允许使用多种途径访问它； 一种方便的途径是使用经典的 choose 操作符，如下所示。

variable {α β : Type*} [Inhabited α]

#check (default : α)

variable (P : α → Prop) (h : ∃ x, P x)

#check Classical.choose h

example : P (Classical.choose h) :=
  Classical.choose_spec h

给定 h : ∃ x, P x, 则 Classical.choose h 的值是某个满足 P x 的 x. 定理 Classical.choose_spec h 表明 Classical.choose h 符合要求。

有了这些，我们就可以定义反函数如下：

noncomputable section

open Classical

def inverse (f : α → β) : β → α := fun y : β ↦
  if h : ∃ x, f x = y then Classical.choose h else default

theorem inverse_spec {f : α → β} (y : β) (h : ∃ x, f x = y) : f (inverse f y) = y := by
  rw [inverse, dif_pos h]
  exact Classical.choose_spec h

之所以需要 noncomputable section 和 open Classical 这两行， 是因为我们正在以一种重要的方式使用经典逻辑。 在输入 y 时， 函数 inverse f 返回某个满足 f x = y 的 x 值（如果有的话）， 否则返回一个缺省的 α 元素。 这是一个 dependent if 结构的实例， 因为在正例中， 返回值 Classical.choose h 取决于假设 h. 给定 h : e 时， 等式 dif_pos h 将 if h : e then a else b 改写为 a, 同样，给定 h : ¬ e, dif_neg h 将它改写为 b. 也有适用于非依赖性条件构造的 if_pos 和 if_neg, 将在下一节使用。 定理 inverse_spec 表明 inverse f 满足这一设定的第一部分。

如果你还不完全理解它们的工作原理，也不用担心。 仅 inverse_spec 定理就足以说明， 当且仅当 f 是单射时， inverse f 是左逆， 当且仅当 f 是满射时， inverse f 是右逆。 通过在 VS Code 双击或右键单击 LeftInverse 和 RightInverse, 或使用命令 #print LeftInverse 和 #print RightInverse, 可以查看它们的定义。 然后尝试证明这两个定理。它们很棘手！ 在开始深入细节之前，先在纸上做证明会有帮助。 每个定理都能用大约六行短代码证明。 如果你想寻求额外的挑战， 可以尝试将每个证明压缩成单行证明。

variable (f : α → β)

open Function

example : Injective f ↔ LeftInverse (inverse f) f :=
  sorry

example : Surjective f ↔ RightInverse (inverse f) f :=
  sorry

在本节的最后，我们将从类型论的角度来阐述康托尔的著名定理， 即不存在从集合到其幂集的满射函数。 看看你是否能理解这个证明，然后填上缺失的两行。

theorem Cantor : ∀ f : α → Set α, ¬Surjective f := by
  intro f surjf
  let S := { i | i ∉ f i }
  rcases surjf S with ⟨j, h⟩
  have h₁ : j ∉ f j := by
    intro h'
    have : j ∉ f j := by rwa [h] at h'
    contradiction
  have h₂ : j ∈ S
  sorry
  have h₃ : j ∉ S
  sorry
  contradiction

4.3. 施罗德-伯恩斯坦定理

我们用一个初等而非平凡的定理结束本章。 令 \(\alpha\) 和 \(\beta\) 是集合。 （在我们的形式化中, 它们实际上会是类型。） 假定 \(f : \alpha → \beta\) 和 \(g : \beta → \alpha\) 都是单射。 直观上，这意味着 \(\alpha\) 不大于 \(\beta\), 反之亦然。 如果 \(\alpha\) 和 \(\beta\) 是有限的， 这意味着它们具有相同的基数，而这相当于说它们之间存在双射。 在十九世纪，康托尔（Cantor）指出，即使当 \(\alpha\) 和 \(\beta\) 无穷时， 同样的结果也成立。 这个结果最终由戴德金（Dedekind）、施罗德（Schröder）和伯恩斯坦（Bernstein）各自独立证明。

我们的形式化将引入一些新方法，我们将在接下来的章节中更详细地解释这些方法。 不必担心它们在这里讲得太快。 我们的目标是向你展示你已经具备为真实数学结果的形式证明做出贡献的技能。

为了理解证明背后的思想，考虑映射 \(g\) 在 \(\alpha\) 中的像。 在这个像中， \(g\) 的逆有定义，且是到 \(\beta\) 的双射。

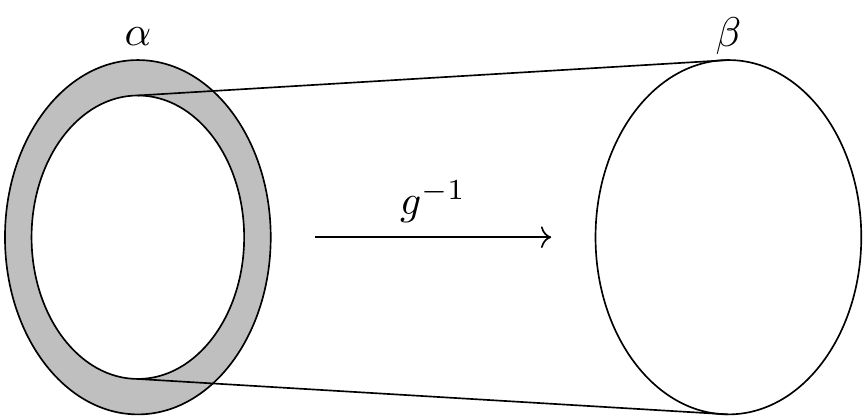
问题是双射不包括图中的阴影区域， 如果 \(g\) 不是满射，则它是非空的。 或者，我们可以使用 \(f\) 把整个 \(\alpha\) 映射到 \(\beta\), 但在那种情况下问题是若 \(f\) 不是满射， 则它会错过 \(\beta\) 的一些元素。

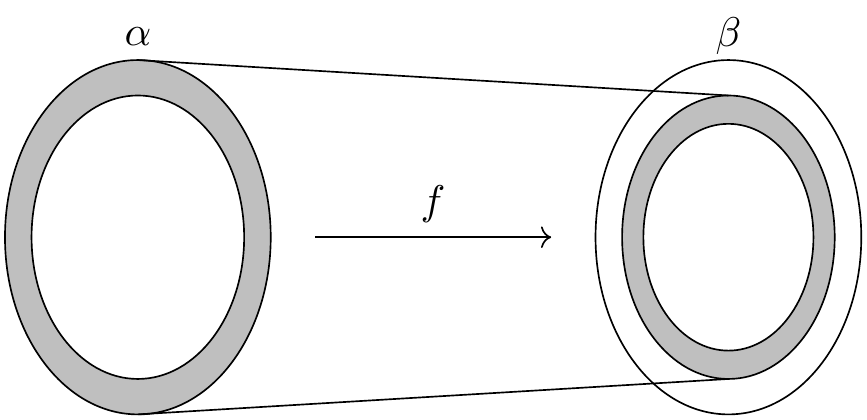
但现在考虑从 \(\alpha\) 到自身的复合映射 \(g \circ f\). 由于这个复合映射是单射，它构成了 \(\alpha\) 和它的像的双射， 在 \(\alpha\) 内部产生了一个缩小的副本。

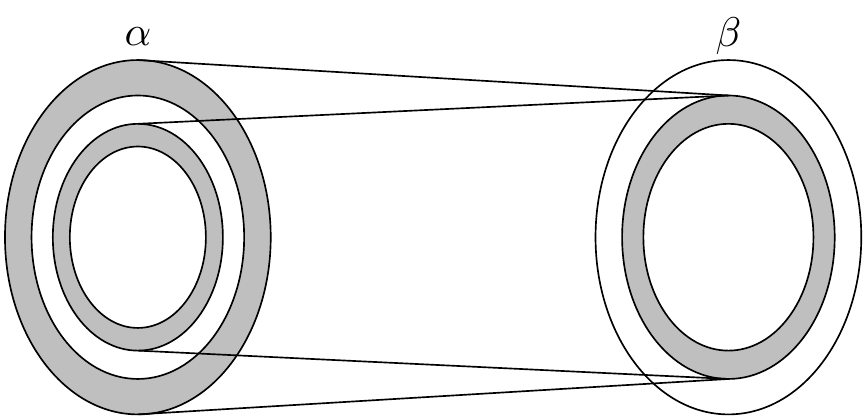
这个复合将内部阴影环映射到另一个这样的集合， 我们可以将其视为更小的同心阴影环，依此类推。 这会产生一个阴影环的同心序列，每个都与下一个有双射对应。 如果我们把每个环映射到下一个，并保留 \(\alpha\) 的无阴影部分， 则我们有 \(\alpha\) 和 \(g\) 的像之间的双射。 和 \(g^{-1}\) 复合，这产生了所需的 \(\alpha\) 和 \(\beta\) 的双射。

我们可以更简单地描述这个双射。 令 \(A\) 为这列阴影区域的并， 如下定义 \(h : \alpha \to \beta\):

\[\begin{split}h(x) = \begin{cases} f(x) & \text{if $x \in A$} \\ g^{-1}(x) & \text{otherwise.} \end{cases}\end{split}\]

换句话说，我们在阴影部分使用 \(f\), 而在其余部分使用 \(g\) 的逆。 生成的映射 \(h\) 是单射， 因为每个分支都是单射并且两个分支的像是不相交的。 为了看出它是满射， 假设给定了 \(\beta\) 中的元素 \(y\), 考虑 \(g(y)\). 若 \(g(y)\) 位于阴影区域之一， 它不能在第一个环中，因此我们有 \(g(y) = g(f(x))\), 其中 \(x\) 在上一个环中。 由 \(g\) 的单射性，我们有 \(h(x) = f(x) = y\). 若 \(g(y)\) 不在阴影区域中， 那么由 \(h\) 的定义，我们有 \(h(g(y))= y\). 不论哪种情况， \(y\) 都在 \(h\) 的像中。

这个论证听起来应该有道理，但细节却很微妙。 形式化证明不仅可以提高我们对结果的信心， 还可以帮助我们更好地理解它。 因为证明使用经典逻辑， 所以我们告诉 Lean， 我们的定义通常是不可计算的。

noncomputable section
open Classical
variable {α β : Type*} [Nonempty β]

记号 [Nonempty β] 规定 β 非空。 我们使用它是因为我们将用于构造 \(g^{-1}\) 的 Mathlib 原语要求它。 定理在 \(\beta\) 为空的情形是平凡的， 虽然把形式化推广到覆盖这种情况并不难，我们不这么做。 特别地，我们需要假设 [Nonempty β] 以使用 Mathlib 中定义的运算 invFun. 对于给定的 x : α, 如果有的话， invFun g x 选择 x 在 β 中的一个原像， 否则就返回 β 中的任意元素。 若 g 是单射，则 invFun g 一定是左逆， 若 g 是满射，则它是右逆。

#check (invFun g : α → β)
#check (leftInverse_invFun : Injective g → LeftInverse (invFun g) g)
#check (leftInverse_invFun : Injective g → ∀ y, invFun g (g y) = y)
#check (invFun_eq : (∃ y, g y = x) → g (invFun g x) = x)

我们定义对应于阴影区域的并的集合如下。

variable (f : α → β) (g : β → α)

def sbAux : ℕ → Set α
  | 0 => univ \ g '' univ
  | n + 1 => g '' (f '' sbAux n)

def sbSet :=
  ⋃ n, sbAux f g n

定义 sbAux 是 递归定义 的一个例子， 我们将在下一章解释。 它定义了一列集合

\[\begin{split}S_0 &= \alpha ∖ g(\beta) \\ S_{n+1} &= g(f(S_n)).\end{split}\]

定义 sbSet 对应于我们的证明概要中的集合 \(A = \bigcup_{n \in \mathbb{N}} S_n\). 上面描述的函数 \(h\) 现在定义如下：

def sbFun (x : α) : β :=
  if x ∈ sbSet f g then f x else invFun g x

我们将需要这样的事实：我们定义的 \(g^{-1}\) 是 \(A\) 的补集上的右逆， 也就是说，是 \(\alpha\) 中无阴影区域上的右逆。 这是因为最外层的环 \(S_0\) 等于 \(\alpha \setminus g(\beta)\), 因此 \(A\) 的补集包含于 \(g(\beta)\) 中。 所以，对 \(A\) 的补集中的每个 \(x\), 存在 \(y\) 使得 \(g(y) = x\). （由 \(g\) 的单射性，这个 \(y\) 是唯一的， 但下一个定理只说了 invFun g x 返回 y 使得 g y = x.）

逐步完成下面的证明，确保你理解发生了什么， 并填写剩余部分。 你需要在最后使用 invFun_eq. 请注意，此处用 sbAux 重写替换了 sbAux f g 0 与相应定义方程的右侧。

theorem sb_right_inv {x : α} (hx : x ∉ sbSet f g) : g (invFun g x) = x := by
  have : x ∈ g '' univ := by
    contrapose! hx
    rw [sbSet, mem_iUnion]
    use 0
    rw [sbAux, mem_diff]
    sorry
  have : ∃ y, g y = x := by
    sorry
  sorry

我们现在转向证明 \(h\) 是单射。 非正式地说，证明过程如下。 首先，假设 \(h(x_1) = h(x_2)\). 若 \(x_1\) 在 \(A\) 中， 则 \(h(x_1) = f(x_1)\), 且我们可以证明 \(x_2\) 在 \(A\) 中如下。 若非如此，则我们有 \(h(x_2) = g^{-1}(x_2)\). 由 \(f(x_1) = h(x_1) = h(x_2)\) 我们有 \(g(f(x_1)) = x_2\). 由 \(A\) 的定义，既然 \(x_1\) 在 \(A\) 中， \(x_2\) 同样在 \(A\) 中，矛盾。 因此，若 \(x_1\) 在 \(A\) 中，则 \(x_2\) 也在， 这种情况下我们有 \(f(x_1) = h(x_1) = h(x_2) = f(x_2)\). \(f\) 的单射性推出 \(x_1 = x_2\). 对称论证表明若 \(x_2\) 在 \(A\) 中， 则 \(x_1\) 也在，这又一次蕴含着 \(x_1 = x_2\).

剩下的唯一可能性是 \(x_1\) 和 \(x_2\) 都不在 \(A\) 中。 这种情况下，我们有 \(g^{-1}(x_1) = h(x_1) = h(x_2) = g^{-1}(x_2)\). 两边使用 \(g\) 就得到 \(x_1 = x_2\).

我们再次鼓励你逐步完成以下证明，观察这个论证在 Lean 中是如何展开的。 看看你是否可以使用 sb_right_inv 结束证明。

theorem sb_injective (hf : Injective f) : Injective (sbFun f g) := by
  set A := sbSet f g with A_def
  set h := sbFun f g with h_def
  intro x₁ x₂
  intro (hxeq : h x₁ = h x₂)
  show x₁ = x₂
  simp only [h_def, sbFun, ← A_def] at hxeq
  by_cases xA : x₁ ∈ A ∨ x₂ ∈ A
  · wlog x₁A : x₁ ∈ A generalizing x₁ x₂ hxeq xA
    · symm
      apply this hxeq.symm xA.symm (xA.resolve_left x₁A)
    have x₂A : x₂ ∈ A := by
      apply _root_.not_imp_self.mp
      intro (x₂nA : x₂ ∉ A)
      rw [if_pos x₁A, if_neg x₂nA] at hxeq
      rw [A_def, sbSet, mem_iUnion] at x₁A
      have x₂eq : x₂ = g (f x₁) := by
        sorry
      rcases x₁A with ⟨n, hn⟩
      rw [A_def, sbSet, mem_iUnion]
      use n + 1
      simp [sbAux]
      exact ⟨x₁, hn, x₂eq.symm⟩
    sorry
  push_neg at xA
  sorry

这个证明引入了一些新策略。 首先，请注意 set 策略， 它引入了缩写 A 和 h 分别代表 sbSet f g 和 sb_fun f g. 我们把对应的定义式命名为 A_def 和 h_def. 这些缩写是定义性的，也就是说， 当需要时，Lean有时会自动展开它们。 但并不总是如此；例如，当使用 rw 时， 我们通常需要精确地使用 A_def 和 h_def. 所以这些定义带来了一个权衡： 它们可以使表达式更短并且更具可读性， 但它们有时需要我们做更多的工作。

一个更有趣的策略是 wlog 策略， 它封装了上面非正式证明中的对称性论证。 我们现在不会详细讨论它，但请注意它恰好做了我们想要的工作。 如果将鼠标悬停在该策略上，你可以查看其文档。

满射性的论证甚至更容易。 给定 \(\beta\) 中的 \(y\), 我们考虑两种情况，取决于 \(g(y)\) 是否在 \(A\) 中。 若是，则它不会在最外层的环 \(S_0\) 中， 因为根据定义，这个环和 \(g\) 的像不相交。 因此存在 \(n\) 使得 g(y) 是 \(S_{n+1}\) 的元素。 这意味着它形如 \(g(f(x))\), 其中 \(x\) 在 \(S_n\) 中。 由 \(g\) 的单射性，我们有 \(f(x) = y\). 在 \(g(y)\) 属于 \(A\) 的补集的情况， 我们立刻得到 \(h(g(y))= y\), 证毕。

我们再次鼓励您逐步完成证明并填写缺失的部分。 策略 rcases n with _ | n 分解为情况 g y ∈ sbAux f g 0 和 g y ∈ sbAux f g (n + 1). 在两种情况下，通过 simp [sbAux] 调用化简器都会应用 sbAux 的相应定义式。

theorem sb_surjective (hg : Injective g) : Surjective (sbFun f g) := by
  set A := sbSet f g with A_def
  set h := sbFun f g with h_def
  intro y
  by_cases gyA : g y ∈ A
  · rw [A_def, sbSet, mem_iUnion] at gyA
    rcases gyA with ⟨n, hn⟩
    rcases n with _ | n
    · simp [sbAux] at hn
    simp [sbAux] at hn
    rcases hn with ⟨x, xmem, hx⟩
    use x
    have : x ∈ A := by
      rw [A_def, sbSet, mem_iUnion]
      exact ⟨n, xmem⟩
    rw [h_def, sbFun, if_pos this]
    apply hg hx

  sorry

我们现在可以把它们放在一起。 最后的论证简短而甜美，证明使用了 Bijective h 展开为 Injective h ∧ Surjective h 这一事实。

theorem schroeder_bernstein {f : α → β} {g : β → α} (hf : Injective f) (hg : Injective g) :
    ∃ h : α → β, Bijective h :=
  ⟨sbFun f g, sb_injective f g hf, sb_surjective f g hg⟩